PENERAPAN KONSEP BANGUN RUANG SISI DATAR DALAM PEMECAHAN MASALA
Assalamualaikum wr. wb.
Bagaimana kabar kalian, semoga dalam keadaan yang sehat dan bahagia yaa. Jangan lupa berdoa dulu sebelum belajar.
Setelah mempelajari luas permukaan dan volume dari masing-masing kubus, balok, prisma dan limas. kali ini kita akan mempelajari tentang penerapan konsep bangun ruang sisi datar pada pemecahan masalah. Tapi sebelum itu, kita pelajari materi gabungan dari beberapa bangun ruang sisi datar.
GABUNGAN BANGUN RUANG SISI DATAR
Perhatikan kandang burung di samping. Kandang burung ini dibuat sangat unik dan menarik. Bentuk ini merupakan perpaduan antara bangun ruang sederhana. Kombinasi bentuk yang digunakan berupa bangun limas dan balok. Sungguh menarik, bukan? Dalam subbab ini akan dipelajari tentang gabungan bangun ruang sisi sederhana yang meliputi kubus, balok, prisma dan limas. Kamu akan mempelajari cara menentukan luas dan volume gabungan bangun ruang sisi datar. Untuk itu pelajari subbab ini dengan sungguh-sungguh.
A. Gabungan Kubus dengan Balok
Bangun di bawah ini terbentuk dari balok dan kubus, dengan demikian volume bangun:
V = V.balok + V.kubus
Berdasarkan gambar, tutup/atas kubus dapat mengganti atau menutupi alas kubus sehingga dapat diartikan bahwa balok mempunyai luas permukaan yang utuh. Akibatnya pada kubus, permukaannya tinggal selimutnya saja. Dengan demikian luas permukaan bangun dapat dituliskan:
L = L.balok + L.selimut kubus
B. Gabungan Kubus/Balok dengan Prisma
Bangun di bawah ini terbentuk dari balok dan prisma, dengan demikian volume bangun:
V = V.balok + V.prisma
Luas permukaan suatu bangun merupakan luas bagian luar yang tampak dari bangun tersebut. Sehingga luas permukaan bangun di bawah dapat dituliskan:
L = L.balok tanpa tutup + 2 × L. alas prisma (segitiga) + L.muka prisma (selimut prisma yang terlihat)
C. Gabungan Kubus/Balok dengan Limas
Bangun di samping terbentuk dari kubus dan limas, dengan demikian rumus volume dan luas permukaannya dapat ditulis sebagai berikut.
V = V.kubus + V.limas
L = L.kubus tanpa tutup + L.selimut limas
D. Gabungan Prisma dengan Limas
Bangun di bawah terbentuk dari prisma dan limas, dengan demikian rumus volume dan luas permukaannya dapat ditulis sebagai berikut.
V = V.prisma + V.limas
L = L.prisma tanpa tutup + L.selimut limas
CONTOH:
1. Tentukan luas permukaan dan volume bangun di samping.
Jawaban:
Sebelum menentukan luas permukaan dan volume, tentukan terlebih dahulu ukuran-ukuran yang terdapat pada bangun tersebut.
Perhatikan segitiga JFG.
IL = JK = 10 - 6 = 4 cm
FK = KG sehingga FK = 1/2 FG = 1/2 × 6 = 3 cm
Segitiga JFK siku-siku di K
Menentukan luas bangun:
L = 2 × L.ADHE + L.selimut
= 2×(AD×AE+1/2×EH×IL)+(AD+DH+HI+IE+EA)×AB
= 2×(6×6+1/2×6×4)+(6+6+5+5+6)×15
= 2×(36+12)+(28×15) = 96+420 = 516 cm2
Menentukan volume bangun:
V = L.ADHE × AB = 48 × 15 = 720 cm3
Jadi, luas permukaan bangun 516 cm2 dan volume bangun 720 cm3
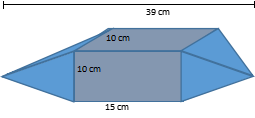
2. Sebuah bangun ruang terdiri atas balok dan limas segi empat beraturan. Kedua limas tersebut berukuran sama. Bangun ruang tersebut disajikan sebagai berikut.
Tentukan volume dan luas permukaan bangun tersebut.
Jawaban:
Balok mempunyai ukuran panjang (p) = 15 cm, lebar (l) = 10 cm, dan tinggi (t.balok) = 10 cm. Tinggi limas (t.limas) = (39-15) : 2 = 12 cm.
Volume bangun
V.bangun = V.balok + 2V.limas
= p×l×t.balok+2×(⅓×l×t.balok)×t.limas
= 15×10×10+2×(⅓×10×10)×12
= 1500 + 800 = 2300
Jadi volume bangun adalah 2.300 cm3.
Luas permukaan bangun
Perhatikan limas pada bangun di samping.
Limas pada bangun mempunyai tinggi = OT = 12 cm
Panjang OE = 1/2 AD = 1/2 × 10 = 5
Perhatikan segitiga EOT siku-siku di O.
Menentukan panjang ET
Menentukan luas bangun:
L.bangun = L.selimut bangun + 2L.selimut limas
= 4 × (p × t) + 2 × (4 × 1/2 × DC × ET)
= 4 × (15 × 10) + 2 × (4 × 1/2 × 12 × 13)
= 600 + 624
= 1224 cm2
Jadi, luas permukaan bangun adalah 1224 cm2
PENERAPAN KONSEP BANGUN RUANG SISI DATAR DALAM PEMECAHAN MASALAH
Dalam kehidupan sehari-hari terdapat soal-soal yang dapat diselesaikan dengan menerapkan konsep bangun ruang sisi datar. Dalam menyelesaiakan soal-soal tersebut, sebaiknya dibuat terlebih dahulu sketsa yang menggambarkan keadaan pada soal. Untuk lebih jelasnya, pelajarilah beberapa contoh soal berikut.
1. Seorang siswa akan membuat kerangka sebuah balok dari seutas kawat. Apabila ukuran kerangka balok itu 12 cm × 8 cm × 4 cm, tentukanlah panjang kawat yang diperlukan.
Pembahasan:
Panjang kawat yang diperlukan sama dengan jumlah rusuk-rusuk balok.
Jumlah rusuk-rusuk balok = 4 × panjang + 4 × lebar + 4 × tinggi
=(4 × 12) + (4 × 8) + (4 × 4) = 48 + 32 + 16 = 96
Jadi, panjang kawat yang diperlukan untuk membuat kerangka itu adalah 96 cm
a. Luas permukaan kotak, dan
b. Volume kotak.
Pembahasan:
a. Luas permukaan kubus tanpa tutup
= 5 × luas bidang yang berusuk 20 cm
= 5 × 202= 5 × 400 = 2000
Jadi, luas permukaan kotak (kubus tanpa tutup) adalah 2000 cm2
b. Perhatikan gambar di samping.
Diketahui panjang rusuk luar kotak = 20 cm dan tebal kayu = 1 cm,
panjang rusuk dalam kotak = 20 cm - 1 cm - 1 cm = 18 cm
Volume kubus = s3 = 183 =5832.cm3
3. Sebuah tenda untuk kemah dibuat berbentuk limas segiempat dengan ukuran seperti terlihat pada gambar di samping ini.
Hitunglah luas bahan yang diperlukan untuk membuat tenda tersebut.
Pembahasan:
Luas bahan yang diperlukan = luas seluruh bidang tegaknya.
Tenda tersebut merupakan sebuah limas yang alasnya berbentuk persegipanjang, sehingga bidang tegaknya terdiri atas 4 buah segitiga yang ukurannya berbeda. Dua buah segitiga berukuran alas 6 m dan tinggi 8 m, sedangkan dua segitiga lainnya berukuran alas 3 m dan tinggi 4 m. Maka:
Luas seluruh bidang tegak = 2 × (1/2 × 6 × 8) + 2 × (1/2 × 3 × 4) = 2× 24 + 2 × 6 = 48 +12 = 60
Jadi, luas bahan yang diperlukan untuk membuat tenda tersebut adalah 60 m2.
Demikian materi penerapan konsep bangun ruang sisi datar. Silahkan kalian kerjakan soal PH 4.9 Bangun ruang sisi datar pada link yang sudah di share di grup WA.
Terima kasih. Semoga bermanfaat.
Wassalaamu 'alaikum Wr Wb
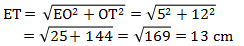
Posting Komentar untuk "PENERAPAN KONSEP BANGUN RUANG SISI DATAR DALAM PEMECAHAN MASALA"