TRIPEL PYTHAGORAS DAN MENENTUKAN JENIS SEGITIGA
TRIPEL PYTHAGORAS DAN MENENTUKAN JENIS
SEGITIGA
Asalamu
‘alaikum Wr Wb…Apa kabar anak – anak kelas 8 ? Semoga kalian semua dalam keadaan sehat dan tetap
semangat aamiin…
Pada pembelajaran hari ini adalah Cara mencari Tripel Pythagoras dan menentukan jenis segitiga . Mari kita mulai terlebih dahulu kita membaca basmalah bersama " Bismillahirrohmanirrohiim"
I.
TRIPEL PYTHAGORAS
Sebelum kalian mencari tripel Pythagoras terlebih dahulu kalian
harus paham dengan pengertian tripel Pythagoras. Apa itu tripel Pythagoras?
Untuk mencari pengertian tripel Pythagoras perhatikan kelompok bilangan berikut
ini.
a) 5, 12, 13
b) 3, 4, 6
Misalkan kelompok tiga bilangan di atas merupakan panjang
sisi-sisi suatu segitiga. Masih ingatkah kalian cara menentukan jenis segitiga dengan teorema Pythagoras?
Nah dengan menggunakan teorema Pythagoras maka kita akan bisa tentukan yang
mana kumpulan bilangan tersebut yang merupakan segitiga siku-siku.
a). misalkan a =
5, b = 12 dan c = 13, dengan
mengkudaratkan sisi miring dan jumlahkan kaudrat sisi lainnya, maka diperoleh:
c2 = 132
c2 = 169
a2 + b2 = 52 +
122
a2 + b2 = 25 + 144
a2 + b2 = 169
Karena 132 = 52 +
122, maka segitiga ini termasuk segitiga siku-siku.
b). misalkan a =
3, b = 4 dan c = 6, dengan
mengkudaratkan sisi miring dan jumlahkan kaudrat sisi lainnya, maka diperoleh:
c2 = 62
c2 = 36
a2 + b2 = 32 +
42
a2 + b2 = 9 + 16
a2 + b2 = 25
Karena 62 >
32 + 42, maka segitiga ini bukan termasuk segitiga
siku-siku.
Dari uraian di atas tampak
bahwa kelompok tiga bilangan 5, 12, 13 merupakan sisi-sisi segitiga siku-siku,
karena memenuhi teorema Pythagoras. Selanjutnya, kelompok tiga bilangan
tersebut disebut tripel Pythagoras.
Jadi, dari penjelasan di atas maka dapat ditarik kesimpulan bahwa pengertian tripel Pythagoras adalah kelompok tiga bilangan bulat positif yang memenuhi kuadrat bilangan terbesar sama dengan jumlah kuadrat dua bilangan lainnya. Bagaimana caranya mencari tripel Pythagoras?
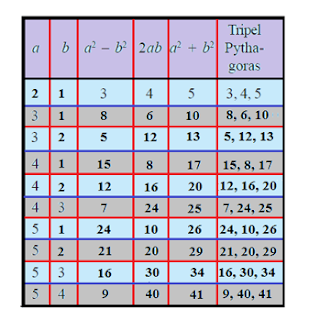
Sekarang perhatikan tabel di
bawah ini.
Tabel di atas merupakan tabel
cara mencari tripel Pythagoras. Dari tabel di atas dapat ditarik kesimpulan
untuk mencari tripel Pythagoras dapat dicari dengan rumus:
(a2 –
b2), 2ab, (a2 + b2)
dengan a > b dan a,
b merupakan bilangan bulat positif.
Contoh
Soal
Pada segitiga ABC diketahui AB
= 10 cm, BC = 24 cm, dan AC = 26 cm. Tunjukkan bahwa ∆ABC siku-siku dan di
titik manakah ∆ABC siku-siku?
Penyelesaian:
Untuk membuktikan
apakah ∆ABC siku-siku dapat digunakan teorema Pythagoras, yakni:
AC2 = 262
AC2 = 676
AB2 + BC2 =
102 + 242
AB2 + BC2 =
100 + 576
AB2 + BC2 =
676
Karena AC2 = AB2 +
BC2, maka ∆ABC termasuk segitiga siku-siku. Jika digambarkan
seperti gambar di bawah ini.
Berdasarkan gambar di atas maka ∆ABC siku-siku di titik B.
II. MENENTUKAN JENIS SEGITIGA BERDASARKAN UKURAN SISINYA
Kebalikan Teorema Pythagoras untuk
Menentukan Jenis Suatu Segitiga
" untuk setiap segitiga jika jumlah kuadrat panjang dua sisi yang saling
tegak lurus sama dengan kuadrat panjang sisi miring maka segitiga tersebut
merupakan segitiga siku-siku".
Pada suatu segitiga berlaku:
a. jika kuadrat sisi miring = jumlah kuadrat sisi yang lain maka segitiga
tersebut siku-siku.
b. jika kuadrat sisi miring < jumlah kuadrat sisi yang lain maka
segitiga tersebut lancip.
c. jika kuadrat sisi miring > jumlah kuadrat sisi yang lain maka
segitiga tersebut tumpul.
CONTOH SOAL
Tentukan jenis segitiga dengan panjang sisi-sisi sebagai berikut.
a. 3 cm, 5 cm, 4 cm
b. 4 cm, 5 cm, 6 cm
c. 1 cm, 2 cm, 3 cm
JAWABAN
Misalkan a = sisi terpanjang , sedangkan b dan c panjang sisi yang lain,
maka diperoleh
a) a = 5 cm, b = 3 cm, c = 4 cm
a² = 5² = 25
b² + c² = 3² + 4² = 9 + 16 = 25
Karena 5²= 3² + 4² maka segitiga ini termasuk jenis segitiga siku-siku.
b). a = 6 cm, b = 4 cm, c = 5 cm
a² = 6² = 36
b² + c² = 4² + 5² = 16 + 25 = 41
Karena 6² < 4² + 5², maka segitiga ini termasuk jenis segitiga lancip.
c). a = 3 cm, b = 1 cm, c = 2 cm
a² = 3² = 9
b² + c²= 1² + 2² = 1 + 4 = 5
Karena 3² > 1² + 2², maka segitiga ini termasuk jenis segitiga tumpul.
Demikian Pembelajaran hari ini, semoga
bermanfaat.Apabila ada di antara kalian yang belum jelas bisa menghubungi bp / ibu
guru kelas masing – masing
Wasalamu’alaikum wr wb







Posting Komentar untuk "TRIPEL PYTHAGORAS DAN MENENTUKAN JENIS SEGITIGA"