NILAI FUNGSI
NILAI FUNGSI
Assalaamu’alaikum Wr Wb…apa kabar anak – anak kelas 8…masih tetap semangat kan ? Pada Pertemuan hari Sabtu ,15 Agustus 2020 kalian sudah mempelajari apa itu Fungsi. Hari ini kita akan melanjutkan ke materi tentang Nilai Fungsi . Yuk…kita mulai saja tetap semangat ya…
1. Notasi Fungsi
Sebelum
kita menghitung nilai fungsi, kita harus mngetahui terlebih dahulu apa yang
dimaksud dengan notasi fungsi, fungsi dinotasikan dengan huruf kecil, seperti
f, g, atau h.
Fungsi f yang memasangkan anggota himpunan A dengan anggota himpunan B dapat
digambarkan sebagai berikut.
Fungsi f yang memasangkan anggota himpunan A dengan anggota himpunan B dapat
digambarkan sebagai berikut.
Dari gambar diagram panah di atas, notasi fungsi f : x→ y= f(x) atau Notasi fungsi f dari A ke B ditulis f: A → B.
Himpunan
A disebut Domain ( Daerah Asal )
Himpunan
B disebut Kodomain ( Daerah Kawan )
Himpunan
C yang memuat y disebut Range ( Daerah
Hasil )
Contoh :
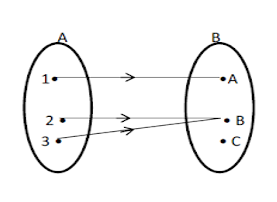
Perhatikan fungsi yang dinyatakan sebagai diagram panah pada gambar berikut !
Contoh :
Perhatikan fungsi yang dinyatakan sebagai diagram panah pada gambar berikut !
Dari gambar di atas maka :
Himpunan A={1,2,3} disebut domain ( Daerah Asal )
Himpunan B={A,B,C} disebut kodomain ( Daerah Kawan )
Hasil pemetaan yaitu {A,B} disebut range ( Daerah Hasil )
2. Menghitung Nilai Fungsi
Perhatikan contoh soal di bawah ini:
Himpunan A={1,2,3} disebut domain ( Daerah Asal )
Himpunan B={A,B,C} disebut kodomain ( Daerah Kawan )
Hasil pemetaan yaitu {A,B} disebut range ( Daerah Hasil )
2. Menghitung Nilai Fungsi
Perhatikan contoh soal di bawah ini:
1.
Diketahui fungsi f: x → 2x – 2 pada himpunan bilangan bulat. Tentukan:
a. f (1)
b. Bayangan (–2) oleh f
c. Nilai f untuk x = –5
d. Nilai x untuk f (x) = 8
e. Nilai a jika f (a) = 14
a. f (1)
b. Bayangan (–2) oleh f
c. Nilai f untuk x = –5
d. Nilai x untuk f (x) = 8
e. Nilai a jika f (a) = 14
Jawab
:
Diketahui f: x → 2x – 2 pada himpunan bilangan bulat.
Dengan demikian rumus fungsinya f (x) = 2x –2.
a. f (1) = 2 (1) – 2 = 0
b. Bayangan (–2) oleh f sama dengan f (–2). Jadi, f (–2) = 2 (–2) – 2 = –6
c. Nilai f untuk x = –5 adalah f (–5) = 2 (–5) – 2 = –12
d. Nilai x untuk f (x) = 8 adalah
2x – 2 = 8
2x = 8 + 2
2x = 10
x = 5
e. Nilai a jika f (a) = 14 adalah
2a – 2 = 14
2a = 14 + 2
2a = 16
a = 8
Diketahui f: x → 2x – 2 pada himpunan bilangan bulat.
Dengan demikian rumus fungsinya f (x) = 2x –2.
a. f (1) = 2 (1) – 2 = 0
b. Bayangan (–2) oleh f sama dengan f (–2). Jadi, f (–2) = 2 (–2) – 2 = –6
c. Nilai f untuk x = –5 adalah f (–5) = 2 (–5) – 2 = –12
d. Nilai x untuk f (x) = 8 adalah
2x – 2 = 8
2x = 8 + 2
2x = 10
x = 5
e. Nilai a jika f (a) = 14 adalah
2a – 2 = 14
2a = 14 + 2
2a = 16
a = 8
2.
Diketahui g: x → 3x + 2 dengan domain {x | – 4 < x ≤ 2, x ∈bilangan bulat} dan
kodomain bilangan bulat.
a. Tuliskan rumus untuk fungsi g.
b. Tuliskan domain g dengan mendaftar anggota-anggotanya.
c. Tentukan daerah hasil g.
kodomain bilangan bulat.
a. Tuliskan rumus untuk fungsi g.
b. Tuliskan domain g dengan mendaftar anggota-anggotanya.
c. Tentukan daerah hasil g.



Posting Komentar untuk "NILAI FUNGSI"